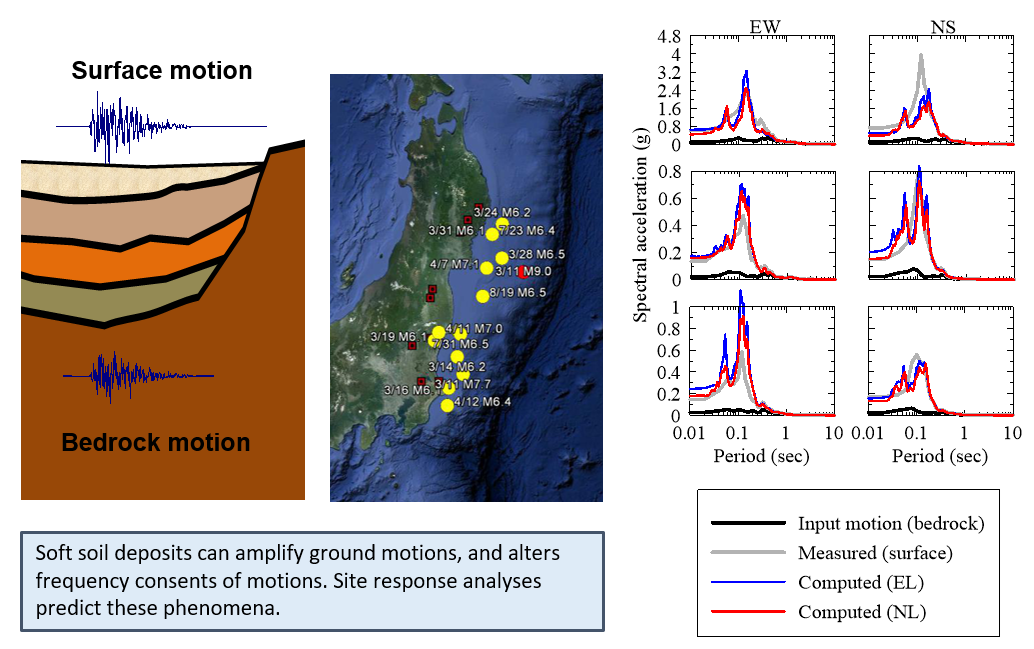
Site response analysis for Japan earthquakes

Published article: Byungmin Kim, and Youssef M.A. Hashash (2013), Site response analysis using downhole array recordings during the March 2011 Tohoku-Oki earthquake and the effect of long-duration ground motions, Earthquake Spectra, v29 (S1), S37-S54

Changes in the intensity and frequency content of earthquake ground motions due to the propagation of the seismic waves through soil deposits are commonly referred to as site effects. One-dimensional (1-D) site response analysis methods are widely used to evaluate these site effects. An increasing number of downhole arrays enable us to better investigate the soil behavior during an earthquake. Long-duration motions during the March 11, 2011, M9.0, subduction zone earthquake near the east coast of Honshu were well recorded. Using these motions, we investigated dynamic soil characteristics and site response due to a long-duration subduction zone earthquake.

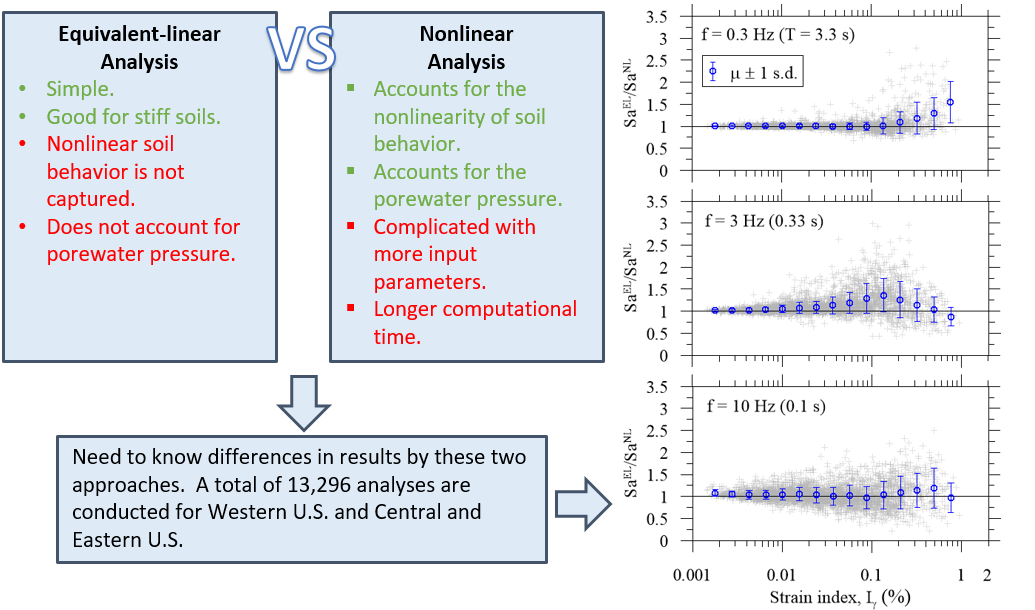
Equivalent-linear vs. nonlinear site response analyses

Sponsored by Next Generation Attenuation Relationship for Central & Eastern North-America (NGA-East)

Published article: Byungmin Kim, Youssef M. A. Hashash, Jonathan P. Stewart, Ellen M. Rathje, Joseph A. Harmon, Michael I. Musgrove, Kenneth W. Campbell, and Walter J. Silva (2016), Relative differences between nonlinear and equivalent-linear site response analyses, Earthquake Spectra, v 32(1), 1845-1865

An equivalent-linear (EL) one-dimensional (1-D) site response analysis simulates the nonlinear response of soil using strain-compatible invariant soil properties. Time domain nonlinear (NL) site response analyses incorporate changes in the soil properties at each time step. The conditions under which the two methods produce consistent and divergent estimates of site amplification are of practical interest due to the advantages and disadvantages of each. We worked on massive site response simulations for both active crustal (Western U.S.) and stable continental regions (Central and Eastern U.S.) using both equivalent-linear and nonlinear analysis methods to investigate the relative differences between these two methods, and to develop guidelines for a priori identification of conditions for which nonlinear method should be considered in lieu of equivalent-linear method.